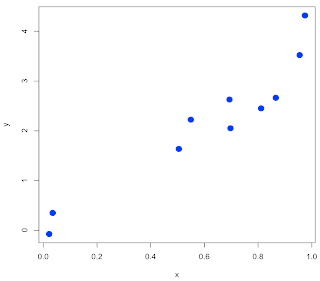
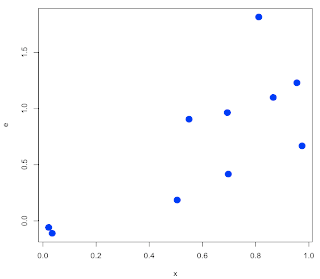
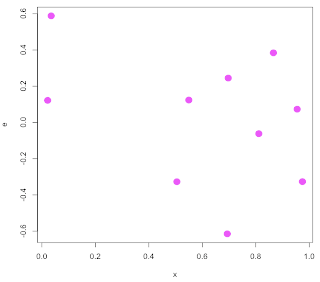
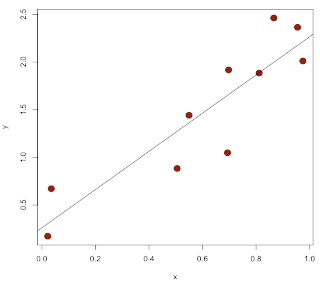
In this case, y(x) = bx so we want
As he says, the key idea is that we can split the first part
and then factor out bx and move it outside the limit:
The term in the limit is something. It depends on what the limit converges too. However, the important thing is that it is not a variable but a constant. Thus,
This is the equation that I used in the last post. Starting from here there is a quick demonstration of something that we proved in a more roundabout fashion before. Start with the equation above and invert it:
but
Beautiful! Strang says "that proof was...powerful too quick." So he does the following.
f(y) converts y to x, it takes the logarithm to base b of x.